Eine Geschichte der Geometrie
Überblick:
Die Anfänge
Die Griechen
Aspekte der Geometrie
Konstruierte oder entdeckte Welt
Die Anfänge
Geometrie (zu deutsch "Vermessung der Erde") ist sicher eine der ältesten
Wissenschaften. Überall dort, wo Ausgrabungen Geschichten prähistorischer
Kulturen in unsere Zeit sprechen lassen, erzählen sie auch eine Geschichte
der Geometrie: regelmäßig oder symmetrisch geformte, bemalte
oder angeordnete Alltags-, Gebrauchs-, oder Ritualgegenstände, zeugen
von dem Erkennen und Übertragen geometrischer Strukturen, die sich
vielfältig in der Natur finden lassen. Kugelähnliche Tongefäße
lassen sich bei gleichem Fassungsvermögen materialsparender und stabiler
herstellen wie quaderförmige, die sich dafür besser schlichten
lassen. Anhand von Gestirnen kann man sich orientieren und bei Malereien
in Höhlen und auf Ton erkennt man Menschen, Tiere und Landschaften
wieder, wenn man sie so verkleinert darstellt, dass die Proportionen
erhalten bleiben.
Auch die mit den ersten Hochkulturen entstehenden Schriftsprachen überliefern
geometrisches Wissen aus Baukunst, Handwerk, Landwirtschaft und Astronomie.
So konnte man in Ägypten nicht nur geradlinig begrenzte Flächen
in rechtwinklige Dreiecke und diese wiederum in Rechtecke flächengleich
umwandeln, auch die Formel für das Volumen allgemeiner Pyramidenstümpfe
war bekannt. Die Umsetzung dieser Kenntnisse in Bauwerken wie den Pyramiden
von Gizeh (ca. 2900 v. Chr.) beeindrucken noch heute:
 die Cheopspyramide, Quelle pixabay
die Cheopspyramide, Quelle pixabay
Aus Millionen tonnenschwerer Steinblöcke wurde die Cheopspyramide
ohne nennenswerte Winkelabweichungen gebaut. Noch geschickter als die Ägypter
waren wahrscheinlich die Babylonier. Sie kannten den sog. "Satz des Pythagoras"
und legten mit ihren Dreiecksuntersuchungen die Grundlagen der Trigonometrie.
Sogar Kreisnäherungen finden sich bei vielen frühen Hochkulturen,
z.B. den Ägyptern, aber auch in der Bibel (z.B. 2.Chronik 4,2). Jedoch
unterschieden die Menschen noch nicht zwischen einer Näherung und
einer exakten Lösung. Auch wurde nur selten der Versuch unternommen,
die Geometrie zu begründen. Geometrisches Wissen war Faktenwissen
zur Lösung konkreter Problemstellungen, aber nicht selbst Gegenstand
der Untersuchung. Es war die Leistung der griechischen Kultur, die Geometrie
auf eine axiomatische Grundlage zu stellen, Näherungen zu analysieren
und Behauptungen zu beweisen. Diese elementaren Methoden, die in der Geometrie
ihren Anfang nahmen, bestimmen nicht nur die Geometrie, sondern die gesamte
Mathematik bis heute.
Die Griechen
Es lässt sich nicht sicher klären, warum manche Griechen
begannen, geometrische Aussagen zu hinterfragen. Bestimmt spielt die griechische
Philosophie- und Diskussionskultur eine entscheidende Rolle: In Streitgesprächen
wurden immer schärfere Maßstäbe angelegt, immer mehr wurde
hinterfragt und man begann Argumente auf logische Fehler zu untersuchen
(vgl. Logik). Diese konstruktive Skepsis machte wohl auch vor der
Geometrie nicht halt und führte in ihrer Präzisierung zum einen
zu den berühmten Beweisen von Pythagoras und seinen Schülern
und zum anderen zu der Formulierung der Euklidschen Geometrie.
 Pythagoras von Samos, Quelle flickr.com
Pythagoras von Samos, Quelle flickr.com
Die Pythagoräer waren eine Sekte, die eine ganz bestimmte Sicht
der Welt hatten. Sie waren unter anderem davon überzeugt, dass
sich die Welt durch Verhältnisse natürlicher Zahlen (also 1,
2, 3, und so weiter) darstellen lässt. Nun zeigte aber ein Mitglied
dieser pythagoräischen Schule, dass es schon bei vielen einfachen
Dreiecken keine gleichlangen Seitenvielfachen gibt: Es gibt z.B. kein ganzzahliges
Vielfaches der Diagonalen eines Quadrates, dass genauso lang ist,
wie ein ganzzahliges Vielfaches der Kantenlänge (heute würde
man sagen: Die Wurzel aus Zwei ist irrational).
Der Geschichte nach soll dieser Ketzer ins Meer geworfen worden sein. Das
Problem war damit aber nicht gelöst. Man begann nun, die Welt nicht
mehr mit Zahlenverhältnissen algebraisch zu beschreiben, sondern geometrisch
und das mit so großem Erfolg, dass man hinter der Geometrie
eine Wirklichkeit zu vermuten begann, deren unvollkommener Schatten unsere
wahrgenommene Welt ist (vgl. Platon). Alle wichtigen Konstruktionen, die
mit Kreisen, Geraden und deren Schnittpunkten (Konstruktionen mit Zirkel
und Lineal) möglich sind und alle wesentlichen Formeln und Sätze
wurden gefunden. Aber es gab schon wieder Probleme, welche sich hartnäckig
einer Lösung entzogen. Man suchte Möglichkeiten, um mit Zirkel
und Lineal zu einem Kreis ein flächengleiches Quadrat zu konstruieren,
einen beliebigen Winkel zu dritteln und aus einer gegebenen Kante eines
Würfels die Kante eines Würfels mit doppeltem Volumen zu konstruieren.
Diese Probleme wurden erst zweitausend Jahre später von Galois wieder
auf die Algebra zurückgeführt, mit deren Hilfe schließlich
gezeigt wurde, dass sich diese Aufgaben mit Zirkel und Lineal gar
nicht lösen lassen. Auch das
Problem der Beschreibung der Diagonalen eines Quadrates mithilfe seiner
Kante wurde erst in dieser Zeit von Dedekind endgültig gelöst.
Doch sowohl die moderne Algebra wie auch die Analysis waren erst möglich
durch eine strengere Formulierung der Mathematik, deren Wegbereiter wieder
griechische Pioniere der Geometrie waren.
 Euklid von Alexandria, Quelle wikipedia
Euklid von Alexandria, Quelle wikipedia
Die Begründung der Euklidschen Geometrie geht auf die "Elemente"
zurück, ein Werk über die Geometrie, das nicht nur Euklids Ideen
darstellt, sondern das geometrische Wissen einer ganzen Epoche (im zweiten,
dritten und vierten Buch findet man z.B. die Ergebnisse der Pythagoräer
wieder). Trotz einiger Schwächen ist bedeutsam, dass im ersten
Buch die Geometrie anhand von Definitionen und Axiomen (vgl. den Logikkurs
zur Erklärung) eingeführt wird, mit deren Hilfe sich anschließend
die geometrischen Sätze ableiten lassen. Geometrische Sätze stehen
nun also nicht mehr zusammenhangslos nebeneinander, sondern werden immer
auf die gleiche Grundlage zurückgeführt, ein Prinzip, dem sich
inzwischen die gesamte Mathematik verschrieben hat. Die Elemente wurden
aus diesem Grund bis in die Neuzeit hinein zu dem Standardwert für
jeden, der Geometrie lernen wollte. Doch nicht nur Euklid leistete einen
entscheidenden Beitrag zur Präzisierung der Geometrie. Im 5. Buch
entwickelt Eudoxos von Knidos seine Proportionenlehre, eine Vorstufe von
Richard Dedekinds "Schnitten" und wie in der Analysis führt das Eudoxos
zu einem ersten quasi analytischen Beweisverfahren, der Exhaustion. Mithilfe dieses indirekten Beweisverfahrens konnte Archimedes,
obwohl "Pi" als reelle Größe nicht zur Verfügung stand, z.B.
das Kugelvolumen finden und gemäß der Euklidschen Geometrie
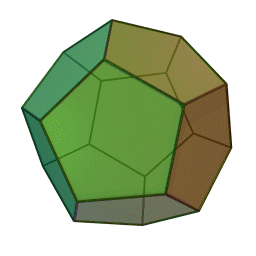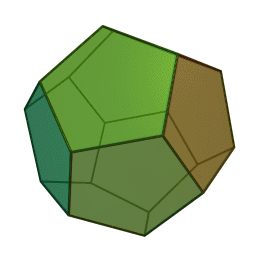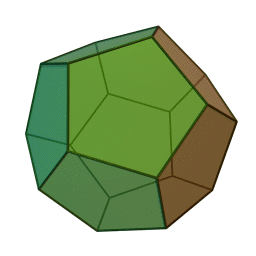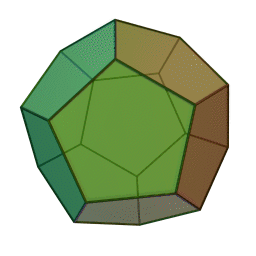
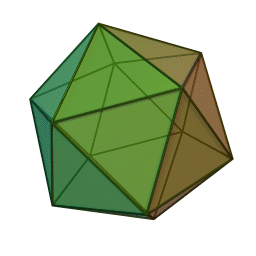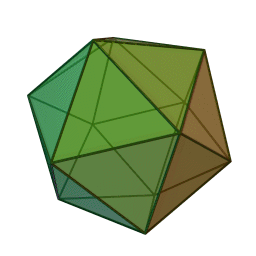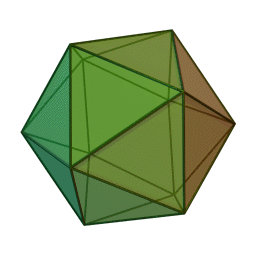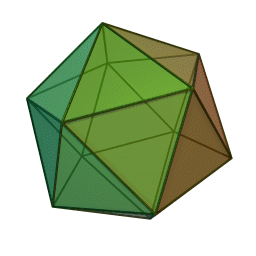
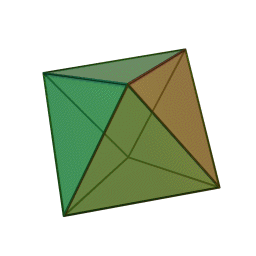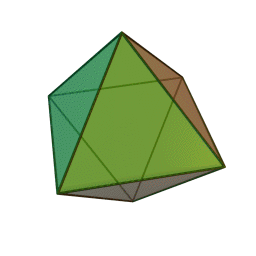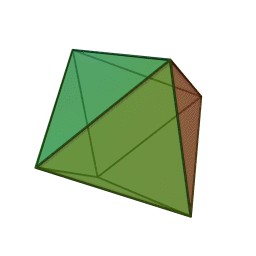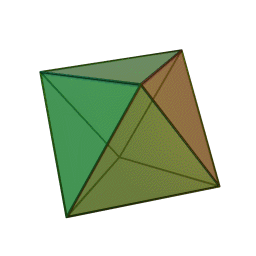
streng beweisen. In den letzen Büchern
der Elemente wird das räumliche Analogon zu den ebenen regelmäßigen
n-Ecken betrachtet, die regulären Körper (Bildquelle wikipedia):
Tetraeder
|
|
Dodekaeder
|
|
Ikosaeder
|
Würfel
|
|
Oktaeder
|
Euklid bewies, dass diese fünf regulären Körper
die einzig möglichen sind. Ein solch
hoher Grad an Symmetrie ist offensichtlich etwas Besonderes. Platon glaubte,
dass die mathematische Struktur des Universums von Symmetrie geprägt
ist und so versuchten viele, aus den regulären Körpern direkt
kosmische Modelle zu entwickeln, wie z.B. Kepler. Als erfolgreicher erwies
sich dagegen, Rotationen und Spiegelungen zu betrachten, welche auf die
regulären Körper aufgrund ihrer Symmetrie keine Auswirkung haben.
Solche gruppentheoretischen Symmetriebetrachtungen
gehören in der physikalische Grundlagenforschung heute mehr denn je
zu den wichtigsten mathematischen Hilfsmitteln.
Doch auch die Griechen wendeten ihre Geometrie bereits an, um sich
eine Vorstellung von der sie umgebenden Welt zu machen. Aristarchos von
Samos wartete, bis der Mond als Halbmond erschien und maß in dem
von Erde, Mond und Sonne aufgespannten rechtwinkligen Dreieck den Winkel
zwischen Mond und Sonne.
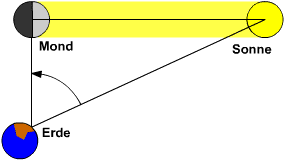
Aus dem Winkel von 87° schloss er, dass die Sonne etwa
20-mal so weit entfernt ist wie der Mond (tatsächlich ist die Sonne
etwa 400-mal so weit entfernt, denn der Winkel beträgt 87°51').
Da bei einer totalen Sonnenfinsternis der Mond die Sonne ziemlich genau
abdeckt, ist nach dem Strahlensatz das Verhältnis der Durchmesser
von Sonne und Mond das gleiche wie das Verhältnis der Abstände
zur Erde. Bei einer Mondfinsternis braucht der Mond etwa die gleiche Zeit,
um in den Erdschatten einzutauchen, wie er anschließend im Erdschatten
verschwunden ist. Daraus schloss Aristarchos, dass die Breite
des Erdschattens dem doppelten Monddurchmesser entspricht und wieder mit
dem Strahlensatz, dass der Mond etwa 40 Erddurchmesser von der Erde
entfernt ist. Später bestimmte Eratostenes mithilfe von Schatten den Erdumfang, so dass sich schließlich
alle Größen in "irdischen" Einheiten bestimmen ließen.
Es war also weit vor unserer Zeitrechnung vielen nicht nur bekannt, dass
die Erde eine Kugel ist um die der Mond als Kugel kreist und dass
die Erde und die anderen Planeten gemeinsam um die Sonne kreisen. Es waren
sogar die geometrischen Methoden bekannt, dieses Sonnensystem zu vermessen
um sich auch Vorstellungen von den kosmischen Größenverhältnissen
zu machen.
Alle geometrischen Leistungen des antiken Griechenlandes aufzuzählen
würde den Rahmen dieser Internetseite sprengen (Trigonometrie, algebraische
Kurven, Kegelschnitte, ...). Es wird jedoch deutlich, wie umfassend und
wirkungsvoll die Maßnahmen einer machtpolitisch pervertierten Kirche
die Weiterentwicklung der Geometrie durch das gesamte Mittelalter hindurch
blockiert haben. Unzählige Entdeckungen und Ideen gingen verloren,
nachdem der Vorhang fiel und Dogmen das Denken ablösten. Vor allem
im indischen und arabischen Raum wurde in dieser Zeit die Mathematik weiterentwickelt.
Die großen Errungenschaften dieser Kulturen liegen im Bereich der
Algebra und der Arithmetik. Die Übernahme dieser mathematischen Erkenntnisse
und die Wiederentdeckung der antiken europäischen Mathematik führte
nach weit über tausend Jahren mathematischen Winterschlafes in Europa
zu einer Renaissance der Geometrie, nachdem Luther zeigte, dass man
auch ohne den Segen des Papstes lesen, denken und glauben kann.
Aspekte der Geometrie
Die algebraischen und arithmetischen Kenntnisse gelangten über
Handelsbeziehungen vom Osmanischen Reich nach Europa, wurden dort jedoch
vorerst kaum weiterentwickelt. Jahrhundertelang wurden in Klöstern neben der
Bibel auch die Elemente immer wieder abgeschrieben und dadurch konserviert. Diese Werke
wurden nach der Reformation durch den neu erfundenen Buchdruck verbreitet und dadurch
außerhalb der Klostermauern wieder entdeckt.
Die in Rückbesinnung auf die antiken Denker von Italien ausgehende Renaissance mit ihrem steigenden Interesse an konkreter Forschung, führte zu höheren Ansprüchen
an die Geometrie und Algebra, die die Beobachtungen beschreiben sollen. Leonardo da Vinci knüpfte an die Kunst- und Wissenschaftstraditionen der Antike an.
 Leonardo da Vinci, Quelle wikipedia
Leonardo da Vinci, Quelle wikipedia
Einen ersten Bruch mit der mittelalterlichen Tradition zugunsten der antiken Tradition führte schließlich Kopernikus herbei,
der das kosmische Modell vereinfachte, indem er, wie Aristarchos, die Erde wieder um die Sonne kreisen ließ. Damit ließen sich die von der Erde aus
beobachteten hässlich komplizierten Schleifen in der Bewegungsbahn des Mars vermeiden und die
Planeten "kreisten" wieder, ganz im Sinne des antiken Aristoteles, für den Kreise als "vollkommen" galten und dem man versuchte gerecht zu werden. Auch Johannes
Kepler versuchte zuerst sein Planetenmodell anhand mystischer Spekulationen
mit den Ideen Aristoteles von Reinheit und Symmetrie in Einklang zu bringen,
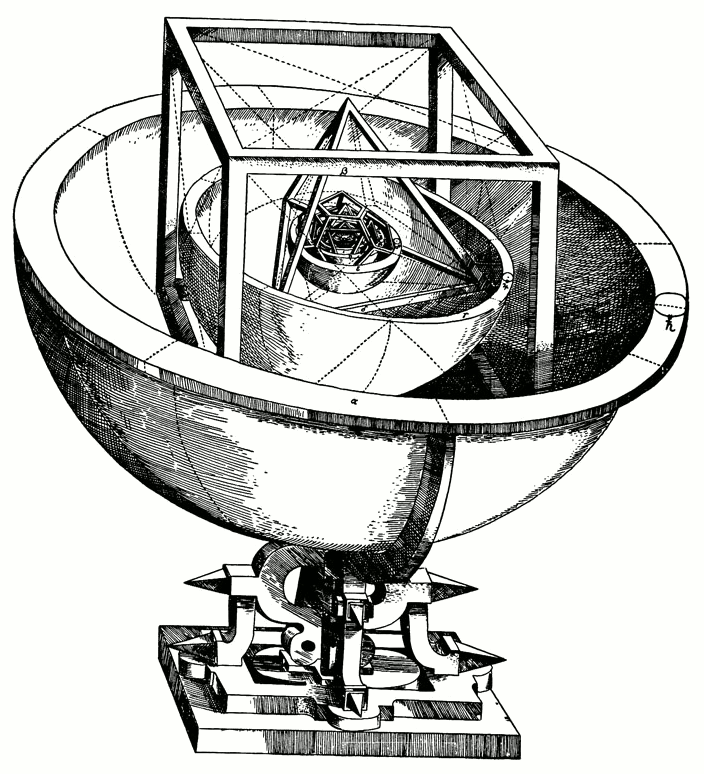 Mysterium Cosmographicum, Quelle wikipedia
Mysterium Cosmographicum, Quelle wikipedia
warf diese Doktrin jedoch schließlich zugunsten seines riesigen
Beobachtungsmaterials über Bord. Seine Beschreibung blieb "geometrisch",
aber die laut Aristoteles "vollkommenen" Kreisbahnen wurden durch "unvollkommene"
Ellipsen abgelöst, die dafür vollkommen den Beobachtungen entsprachen. Die beobachtbare
Welt gewann an Bedeutung gegenüber der antiken Ideenwelt.
Neben der geometrischen Beschreibung der Planetenbahnen als Ellipsen mit
der Sonne in einem ihrer Brennpunkte und der Beobachtung, dass der
Pfeil von der Sonne zum Planeten in gleicher Zeit immer die gleiche Fläche
überstreicht, stellte Kepler auch einen algebraischen Zusammenhang
zwischen den Umlaufzeiten und den Halbachsen her. Nach dem Bruch mit der im
Mittelalter von der Kirche gelehrten Weltsicht kam nun also der Bruch mit der antiken
Metaphysik. Die Idee der anbrechenden Aufklärung war unter anderem, dass der vernunftbegabte Mensch
selbst in der Lage ist, seine Umwelt durch Beobachtung zu verstehen und Gesetze zu erkennen,
welche die Beobachtungen beschreiben und voraussagen. Vor allem Kepler und Galilei fanden eine Fülle
von mechanischen Gesetzen. Es war die Leistung von
Isaak Newton,
 Newton 1689 von Godfrey Kneller, Quelle wikipedia
Newton 1689 von Godfrey Kneller, Quelle wikipedia
hinter den algebraischen und geometrischen Gesetzen die Gesetze der
Mechanik zu entdecken und (unabhängig von Leibniz) die mathematischen
Werkzeuge zu entwickeln, mit denen sich die geometrischen Beobachtungen
voraussagen und interpretieren lassen. So entwickelte Newton die Differentialrechnung,
aus der sich die Analysis entwickelte. Nur mit einer handvoll Gesetzen ließ
sich die Bewegungsbahn eines geworfenen Steins genauso bestimmen, wie die
Bahn von Planeten und Kometen oder später der optimale Weg von Apollo 11 zum Mond.
Umgekehrt konnte von Bahnen auf Kräfte
zurück geschlossen werden. Kurven waren Darstellungen arithmetischer
Zusammenhänge und umgekehrt.
Neben der Entstehung der Analysis zur Beschreibung physikalischer Vorgänge,
wurde die Geometrie in der Renaissance auch in der Kunst genutzt, z.B.
um perspektivisch richtige Darstellungen zu erhalten. Da Vinci und Dürer
nutzen das geometrische Wissen der Antike für ihre Kunstwerke und
in der Kunstausbildung fand die Geometrie mehr und mehr ihren Platz. Nicht
die zeichenbare Kurve rechtfertigte mehr die Existenz der beschreibenden
Formel, sondern die Formel rechtfertigt die Kurve. Räumliche geometrische
Objekte konnten auf Ebenen projiziert werden. Die dabei entstehenden neuen
Kurven erhielten ihre Rechtfertigung aus den Projektionsformeln. Die geometrische
Beschreibung von Projektionen mit Pfeilen wird im Skalarprodukt mit Tupeln
(Beschreibung dieser Pfeile mithilfe von Koordinaten) realisiert. Es entstand
die projektive Geometrie, die Vektoralgebra (wir gehen darauf in der Linearen
Algebra ein) und schließlich die Differentialgeometrie, die diese
projektiven Techniken mit der Analysis verbindet. Monge, ein Vorreiter
dieses neuen Geometrieverständnisses, gründete die École
Polytechnique, eine Elitehochschule, an der unter anderem diese Geometrien
gelehrt und entwickelt wurden.
1827 bewarb sich der damals sechzehnjährige Evariste Galois an
dieser Hochschule. Die Denksperre des Mittelalters war längst durchbrochen,
aber, wie Schiller sagt: "Gegen Dummheit kämpfen Götter selbst
vergebens." - ein Grundproblem bis heute. Galois wurde abgelehnt. Zwar
erahnte später Louis-Paul-Emile Richard die Tragweite von Galois Ideen
und schlug ihn erneut für die École Polytechnique vor, aber
dort wurden seine Arbeiten von keinem geringeren als Cauchy verschlampt.
Galois stellte sich als Achtzehnjähriger erneut der Aufnahmeprüfung
der École Polytechnique und fiel endgültig durch, nachdem er
sich in der mündlichen Prüfung nicht von den falschen Vorstellungen
eines Prüfers überzeugen ließ. Schließlich schickte
er noch eine Abhandlung über die allgemeine Lösung von Gleichungen
an die Akademie der Wissenschaften. Diesmal war es Poisson, der die Arbeit
als "unverständlich" verwarf. Frustriert widmete sich Galois stärker
politischen Zielen, wurde in ein Duell hineingezogen und am 30. Mai 1832
erschossen. Am Vorabend des Duells skizzierte er noch in fieberhafter Eile
sein mathematisches Vermächtnis. Es war die Antwort auf die Kernfragen
der Geometrie und Algebra. Mit seinen Überlegungen ließen sich
auch die jahrtausendealten Fragen nach der Quadratur der Kreises, der
Drittelung des Winkels und der Würfelverdopplung lösen, indem
diese geometrischen Fragen algebraisch formuliert werden. Generationen großer Mathematiker begannen in den Folgejahren Galois Ideen zu Ende zu denken, doch die Gelehrten seiner Zeit verstanden ihn nicht und so wäre er beinahe in der Geschichte
untergegangen.
 Evariste Galois, Quelle wikipedia
Evariste Galois, Quelle wikipedia
Konstruierte oder entdeckte Welt
Ein Problem, das hier bereits angeschnitten wurde, soll als letztes
behandelt werden: Die Frage, ob Mathematik entdeckt oder erfunden wird.
Es ist kein Zufall, dass diese eher philosophische Frage im Zusammenhang
mit der Geometrie aufgegriffen wird, ist doch keine andere mathematische
Disziplin von jeher so eng mit dieser Überlegung verbunden wie die
Geometrie. Es wurde erwähnt, dass Geometrie durchaus in der Natur
entdeckt werden kann, z.B. in der regelmäßigen Formgebung von
Kristallen und Bienenwaben, im kreisrunden Vollmond, im rechten Winkel
zwischen Baum und Erde, in der scheinbaren Ebene des Stillen Ozeans, in
der beobachteten Drehung der Sonne um die Erde, etc.. Es liegt nahe, dass
die Wahrnehmung dieser Welt die frühe Menschheit zur Geometrie brachte.
Doch schon Platon hatte in seiner Ideenlehre die Vermutung, dass die
Geometrie nicht diese Welt abbildet, sondern diese Welt ein Abbild der
Geometrie ist. Geometrie ist aus dieser Sicht nicht etwas beliebig Konstruiertes
(im wahrsten Sinne des Wortes), sondern reine Wahrheit. Aus dieser Sicht
heraus gibt es demnach auch keine Wahlfreiheit bei den Axiomen. Die Euklidschen
Axiome beschreiben so gesehen nur den tiefsten Grund der Wahrheit und sind
deshalb nicht mehr hinterfragbar. Ihre Wahrheit ist an ihrer Schönheit
und Ästhetik zu erkennen. Aber auch anschaulich leuchten die Axiome
ein, sie beschreiben die Wahrnehmung, die Schatten der Wahrheit, die das
Genie überwindet um zur Wahrheit selbst durchzudringen.
Eine Folge dieser Sichtweise war unter anderem der wichtige Abstraktionsschritt von konkret gezeichneten Kreisen und Geraden zu den Ideen von diesen geometrischen Objekten, die durch die Zeichnung nur mehr oder weniger unvollkommen dargestellt werden können. So gesehen lässt sich z.B. eine Winkeldrittelung nicht durch messen erreichen (jedes reale Messinstrument ist unvollkommen und führt zu Messfehlern), sondern nur durch Konstruktionen aus dieser idealen Ideenwelt. Und die Ideenwelt wurde nach damaliger Auffassung in den Axiomen von Euklid beschrieben. Doch all diese
Schönheit und Reinheit hatte bei Euklid einen Makel. Über 2000
Jahre lang war man aus anschaulichen Gründen der Meinung, Euklids Parallelenpostulat sei überflüssig
und mit den anderen Axiomen der Geometrie beweisbar. Wolfgang von Bolyai
schreibt dazu seinem Sohn: "Es ist unbegreiflich, dass diese unabwendbare
Dunkelheit, diese ewige Sonnenfinsternis, dieser Makel an der Geometrie
zugelassen wurde, diese ewige Wolke an jungfräulicher Wahrheit." Doch
schreibt er auch: "Du darfst die Parallelen auf ihrem Wege nicht versuchen;
ich kenne diesen Weg bis an sein Ende - auch ich habe diese bodenlose Nacht
durchmessen, jedes Licht, jede Freude meines Lebens sind in ihr ausgelöscht
worden -, ich beschwöre dich bei Gott, lass die Lehre von den
Parallelen in Frieden (...) Ich hatte mir vorgenommen, mich für die
Wahrheit aufzuopfern; ich wäre bereit gewesen, zum Märtyrer zu
werden, damit ich nur die Geometrie von diesem Makel gereinigt dem menschlichen
Geschlecht übergeben könnte. Schauderhafte, riesige Arbeiten
habe ich vollbracht, habe bei weitem Besseres geleistet, als bisher geleistet
wurde, aber keine vollkommene Befriedigung habe ich je gefunden (...) Ich
bin zurückgekehrt, als ich durchschaut habe, dass man den Boden
dieser Nacht von der Erde aus nicht erreichen kann, ohne Trost, mich selbst
und das ganze Menschengeschlecht bedauernd."
Trotz aller Warnungen seines Vaters versuchte sich auch der Sohn Johann
von Bolyai an dem Parallelenpostulat. Die Versuche zur Widerlegung des
Parallelenpostulates waren bis dahin immer etwa von der Form "Wenn es durch
einen Punkt zu einer Geraden mehr als eine Parallele gibt, dann..." (vgl.
Beweis durch Widerspruch im Logikkurs). Doch der Sohn versuchte schließlich
nicht mehr das Parallelenpostulat zu beweisen. Stattdessen stellten Lobatschewski
und er eine neue "Geometrie" vor, die in allen Axiomen der Euklidschen
Geometrie entsprach, bis auf das Parallelenaxiom. Die neue Geometrie wurde
erst abgelehnt, bis es Klein und Poincaré gelang, sie zu veranschaulichen
(das Problem bleibt, dass Wissenschaftler uns immer neue Modelle der
Welt vorlegen, die immer unvorstellbarer werden). Trotzdem sah man die
Euklidsche Geometrie als überlegen an, beschreibt doch nur sie die
"wirkliche" Welt. Euklid hatte zwar recht mit seiner Forderung des Parallelenaxioms,
aber zumindest waren diese Axiome aus Sicht der mathematischen Öffentlichkeit
nicht beliebig. Und noch mehr: Man musste auch nicht Rechenschaft
ablegen, ob diese Axiome sinnvoll sind. Man musste z.B. nicht überprüfen,
ob die Axiome zu widersprüchlichen Aussagen führen. Schließlich
war ja die der Welt zugrunde liegende Wahrheit die Legitimation der Axiome.
Es war David Hilbert, der an dieser Stelle dem Mythos den Formalismus
entgegenstellte. Seiner Meinung nach sind Aussagen über "Wahrheit"
mathematisch gar nicht zu leisten. Die Mathematik konstruiert im besten
Fall in sich widerspruchsfreie Systeme (in diesem Sinne formulierte er
auch die Euklidsche Geometrie noch einmal). Andere Wissenschaften können
dann, je nach Anwendbarkeit, das eine oder andere System nutzen um zu konsistenten
Aussagen zu gelangen. Im Falle der Astronomie hat sich zum Beispiel gezeigt,
dass die Euklidsche Geometrie, deren Unantastbarkeit über Jahrtausende
hochgehalten wurde, die Wirklichkeit nicht so gut darstellt wie die Riemannsche
Geometrie der allgemeinen Relativitätstheorie. Nun war auch David Hilbert zu optimistisch.
Er ging zumindest noch davon aus, dass jede mathematisch formulierbare
Aussage mithilfe der Mathematik prinzipiell beurteilt werden kann (wenn
auch nicht auf "Wahrheit"). Doch 1931 stellte Kurt Gödel mit Hilfe
primitiv-rekursiver Prädikate eine Formel auf, die ihre eigene Unbeweisbarkeit behauptet. Mit Aussagen dieser
Art brachte schon Bertrand Russell das
schöne Gebäude der Cantorschen Mengenlehre zum Einsturz.
Viele, auch grundlegende Fragen sind noch unbeantwortet. Einerseits
büßte die Geometrie immer mehr ihre Unantastbarkeit ein, andererseits
wurden die Erfolge bei der geometrischen Beschreibung unserer Welt immer
bestechender. Wenn die Mathematik nur ein beliebiges erfundenes Spiel ist,
wieso lässt sie sich dann so vortrefflich anwenden? Auch Heitler
stellt sich diese Frage mit Blick auf die Geometrie: "Welchen Grund sollte
der Planet Merkur haben, sehr genau die Bahn nach der Formel zu verfolgen
(einschließlich der jährlichen Periheldrehung von 43"), die
aus der allgemeinen Relativitätstheorie abgeleitet ist? Er tut es
sicher nicht dem Physiker zu Gefallen. Man kann nicht einfach daran vorbeigehen,
dass das Gesetz ein Naturgesetz ist." Wir stehen also immer noch dort,
wo wir begonnen haben. Wir erkennen, dass diese Welt irgendetwas
mit Geometrie zu tun hat. Wir "wissen" inzwischen mehr über diese Welt
und auch über die Geometrie, aber der eigentliche Zusammenhang bleibt
weiter im Dunkeln.
Die Platonisten berufen sich weiter darauf, dass Mathematik eine eigene Form von Wirklichkeit ist,
die erforscht werden kann. Sie haben sich damit abgefunden, dass es nicht nur eine,
sondern viele solcher Wirklichkeiten gibt, die einander auch widersprechen und somit nur getrennt
voneinander existieren können. Sie mussten sich sogar damit abfinden, dass in vielen dieser Wirklichkeiten
bestimmte Fragen nicht beantwortet werden dürfen und wenn man sie doch beantwortet, muss man andere
Fragen, auf die man bisher eine Antwort hatte, unbeantwortet lassen, um sich nicht in Widersprüchen zu verheddern.
Die Formalisten berufen sich weiter darauf, dass Mathematik eine Aneinanderreihung von Zeichen und Symbolen nach bestimmten willkürlichen Regeln ist, die eben manchmal auch zur Beschreibung der beobachteten Welt nützlich ist. Dass die Mathematik aber auch dann noch erfolgreich ist, wenn sie auf neue Objekte angewandt wird, bleibt aus dieser Sichtweise ein Wunder.
Das Problem ist, etwas tiefer angesetzt, die Frage, inwieweit ein Außen und ein Innen existiert und wie sie abgegrenzt werden können. Mathematik spielt sich in uns ab (oder außerhalb von uns) und wir beobachten eine Welt um uns herum (oder in uns)? Solchen grundsätzlichen Fragen ist nicht beizukommen, erst recht nicht durch Naturwissenschaften oder der Psychologie, denn die setzen dass "außen" bereits voraus (der Psychologe sieht von außen auf das Hirn eines anderen und glaubt deshalb, ein Hirn zu haben, dass die Information "Hirn" verarbeitet). Die Mathematik bleibt hier die Grundlagenwissenschaft.
Und so spielt man sein lieb gewonnenes Spiel weiter, staunend, was dabei aller herauskommt.
"Mathematik kann definiert werden als die Wissenschaft, in der man weder
weiß, wovon man spricht, noch ob das, was man sagt, wahr ist." (Bertrand
Russell)
(Text E. Böhm, 2001)





 die Cheopspyramide, Quelle pixabay
die Cheopspyramide, Quelle pixabay Pythagoras von Samos, Quelle flickr.com
Pythagoras von Samos, Quelle flickr.com Euklid von Alexandria, Quelle wikipedia
Euklid von Alexandria, Quelle wikipedia





 Leonardo da Vinci, Quelle wikipedia
Leonardo da Vinci, Quelle wikipedia Mysterium Cosmographicum, Quelle wikipedia
Mysterium Cosmographicum, Quelle wikipedia Newton 1689 von Godfrey Kneller, Quelle wikipedia
Newton 1689 von Godfrey Kneller, Quelle wikipedia Evariste Galois, Quelle wikipedia
Evariste Galois, Quelle wikipedia